滑らかな加速がしたい(三角関数編)

はじめに

みなさん，台形加速していますか？
僕もしています．

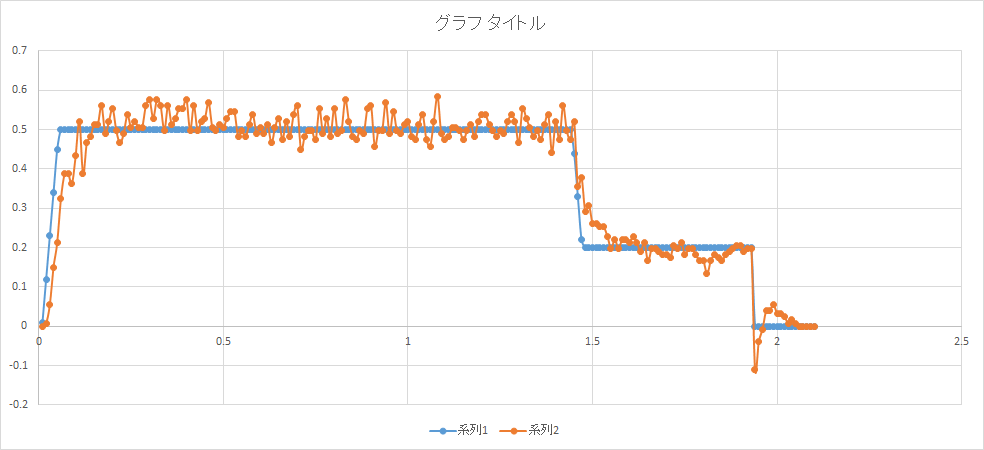
綺麗な目標速度ですね．
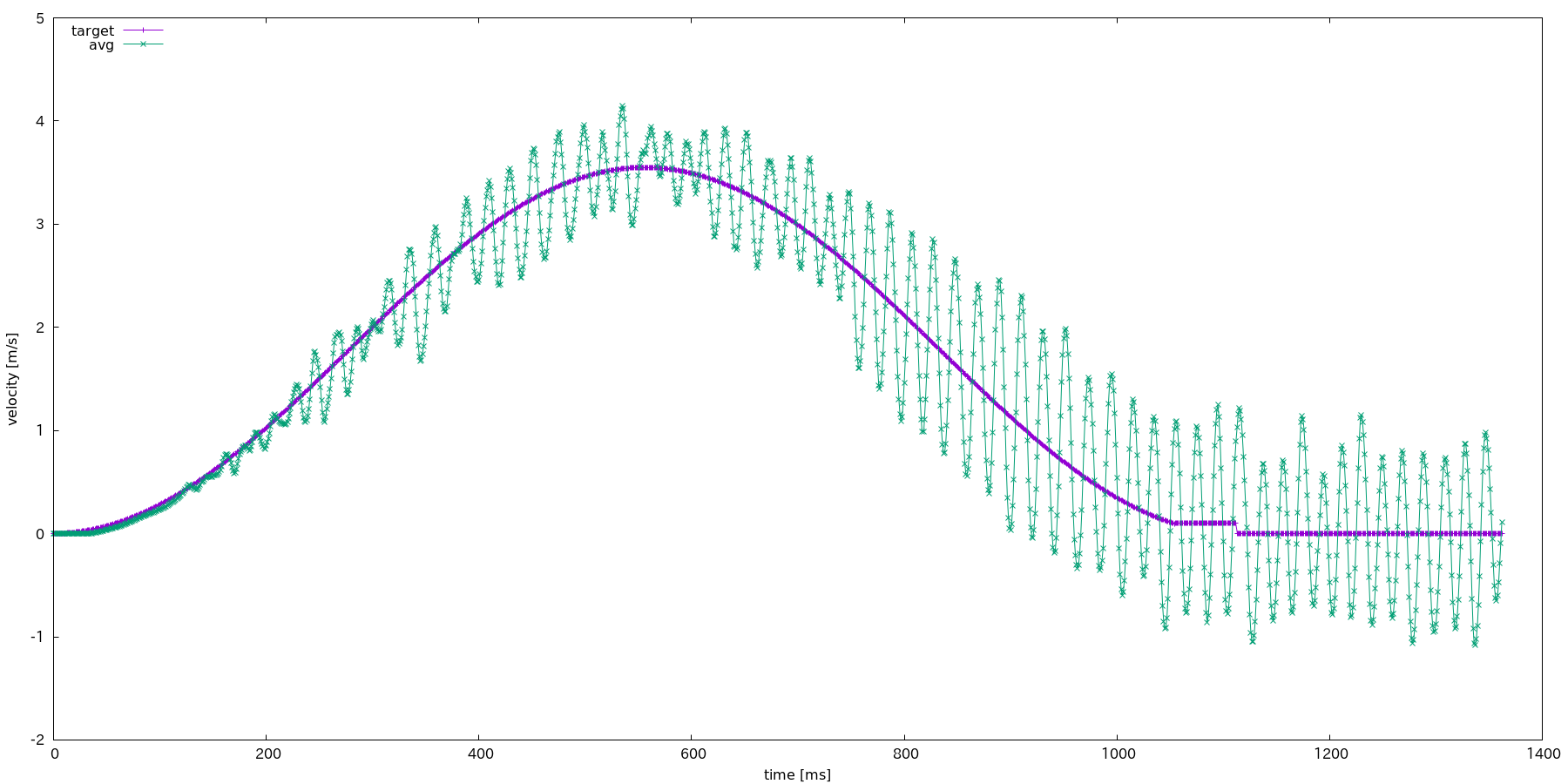
しかし先日「このグラフはありえないよねー」とのツッコミを頂き，滑らかな加減速がしたいなあと思い始めました．
というのも，速度の変化時に微分不可能な部分があるため，追従が悪くなるということだそうです．

今回は，三角関数を用いた加減速についてまとめようとおもいます．

条件

僕の場合，走行するときには次のパラメータを用意します．

• 初速度
• 最高速度
• 終速度
• 最高加速度の絶対値
• 到達目標距離

今回の加減速では三角関数を使うといいましたが，次のような加速・減速になってほしいなあと思いました．

加速のようす(式 )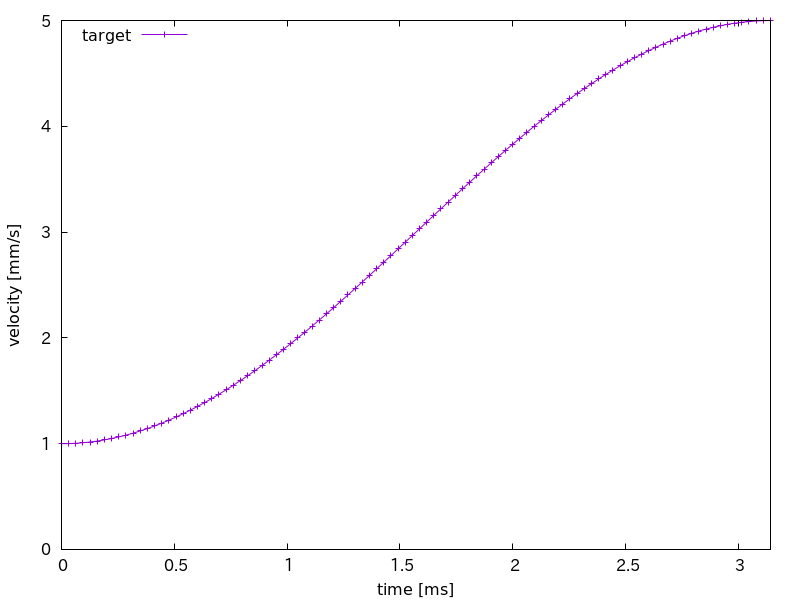

この式の基本形には を使っています．

ただし， としました．

減速のようす(式 )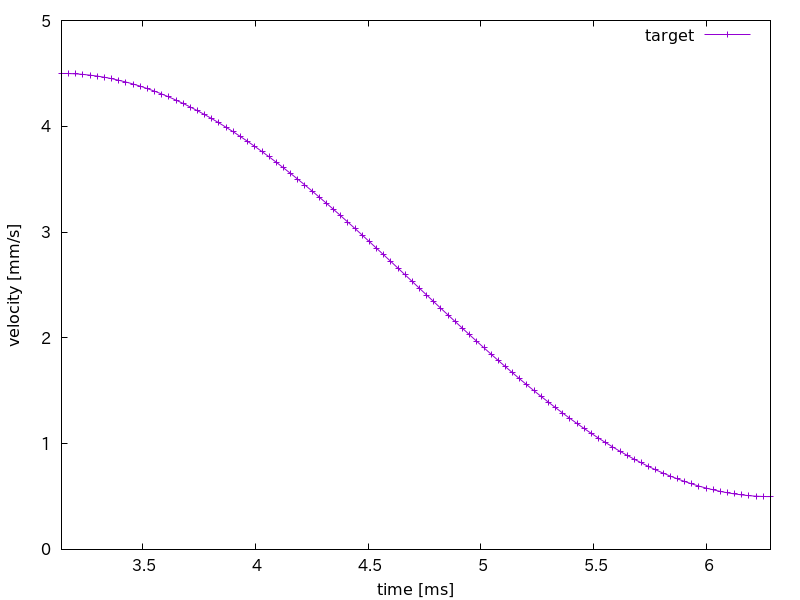

こちらも同様に

ただし， としました．

これらの加減速区間と等速区間を組み合わせて，次のような速度変化にすることが理想形です．

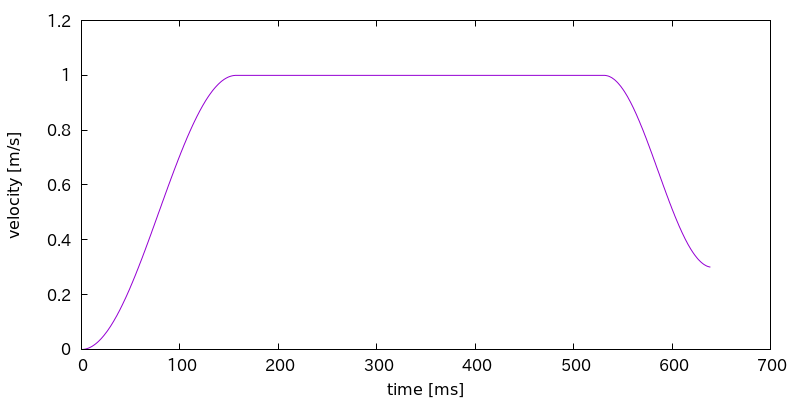
しかし，目標距離が短くて最高速度に達しない場合を考慮する必要があります．
この場合は次のような速度変化になります．

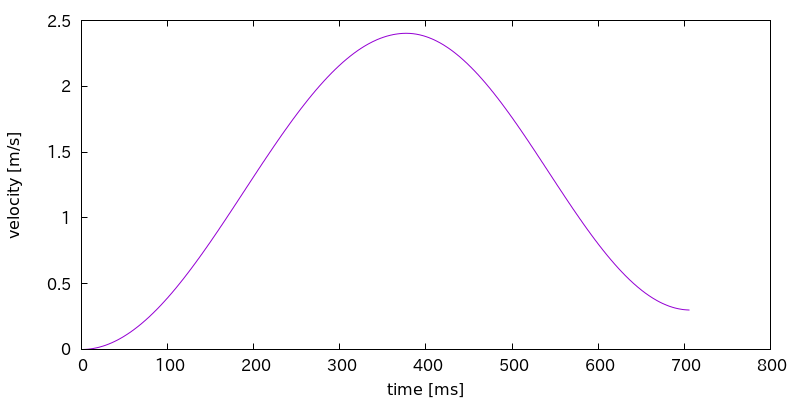
というわけで，
最高速度に達するかどうかの判定をしてから，目標とする加速距離と加速時間・減速距離と減速時間を導出していきます．

ひたすら計算

加速区間と加速時間

与えられたパラメータから，加速に必要な距離と時間を求めます．
ただし，次のように変数を設定します．

• 加速区間(加速に必要な距離)
• 加速時間(加速に必要な時間)
• 等速区間(等速運動し続ける距離)
• 等速時間(等速運動し続ける時間)
• 減速区間(減速に必要な距離)
• 減速時間(減速に必要な時間)

加速時間

これは簡単で，位相が 動く時間であるので，

として導出できました．

加速区間

では，加速に必要な距離を求めます．
先程導出した までの時間で積分をすれば距離が求まります．

減速区間と減速時間

同様に，減速に必要な距離と時間を求めます．

減速時間

として導出できました．

減速区間

では，減速に必要な距離も同様に．

最高速度に達するかどうかの判定

ここで，最高速度に達するかどうかの判定を行います．
次の式が満たされる場合は最高速度に達する，そうでない場合は達しないということになります．

最高速度の設定

先程の式が満たされなかった場合，つまり最高速度の再設定が必要な場合は，次の式から新しい最高速度を求めます．

おわり

きれいな加速ができるようになりました．